Goedel-Prover-V2 : 普林斯顿联合清华等开源的定理证明模型

37 0 0

AI智库导航-aiguide.cc为您提供最新的AI新闻资讯和最新的AI工具推荐，在这里你可以获得用于营销的AI聊天机器人、AI在商业管理中的应用、用于数据分析的AI工具、机器学习模型、面向企业的AI解决方案、AI在商业客户服务中的应用、AI和自动化工具等。

主要介绍

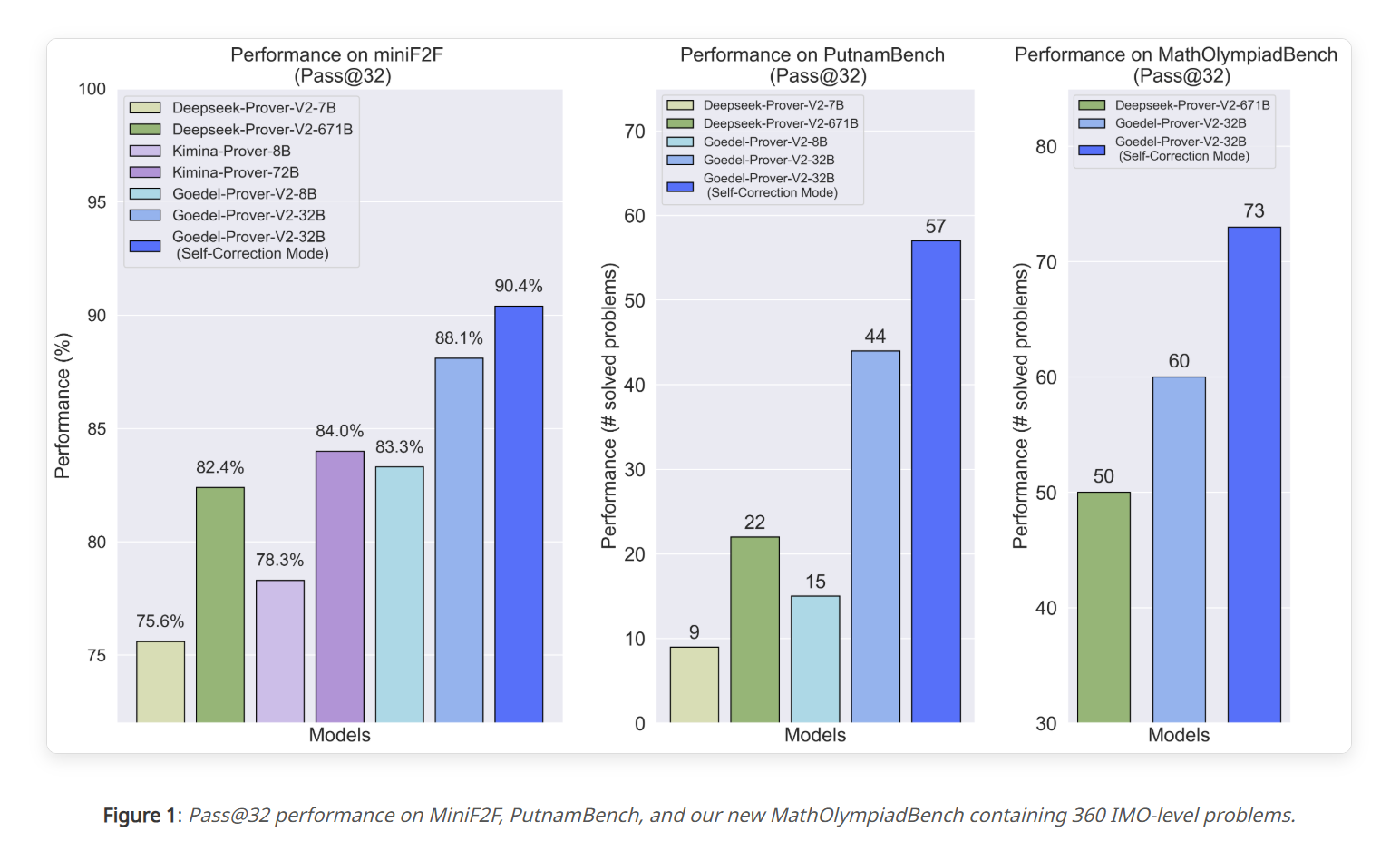
Goedel-Prover-V2 是由普林斯顿大学、清华大学、英伟达、斯坦福等八大顶尖机构联合开发的开源数学定理证明模型，以 Qwen3-8B 和 Qwen3-32B 为基座模型，专注于自动形式化数学定理的生成与验证。其核心目标是通过自动化技术，将自然语言数学问题转化为形式化语言（如 Lean 4），并生成机器可验证的证明，显著提升定理证明效率与可扩展性。该模型在 MiniF2F、PutnamBench、MathOlympiadBench 三大基准测试中全面超越前代 SOTA 模型（如 DeepSeek-Prover-V2-671B），其中 32B 旗舰模型在 MiniF2F 上 Pass@32 正确率达 90.4%，8B 模型性能与参数量近 100 倍的 DeepSeek-Prover-V2-671B 持平，展现了极高的效率与能力。

功能特点

高性能证明生成：在 MiniF2F 基准上，32B 模型 Pass@32 正确率 90.4%，8B 模型达 83.3%，超越所有开源竞品。
低计算开销：在 PutnamBench 基准上，32B 模型仅用 Pass@64 解决 64 道问题，计算效率远超 DeepSeek-Prover-V2-671B 的 Pass@1024 记录。
奥林匹克级难题攻克：在 MathOlympiadBench（含 360 道 IMO 级别题目）上，32B 模型攻克 73 个问题，显著领先于 DeepSeek-Prover-V2-671B 的 50 个。
自我修正能力：通过 Lean 编译器反馈迭代修正证明，两轮修正后总输出长度仅从 32K tokens 增至 40K tokens，保持高效性。

优缺点

优点：
- 参数效率极高：8B 模型性能媲美 671B 模型，推理成本降低近两个数量级。
- 技术突破显著：分层式数据合成、验证器引导修正等技术解决传统模型训练中的数据稀缺与误差累积问题。
- 开源生态友好：模型权重与数据集（如 MathOlympiadBench）完全开源，支持社区协作与二次开发。
缺点：
- 复杂场景稳定性待优化：在极端复杂定理证明中，自我修正的迭代次数可能增加，影响实时性。
- 领域适应性局限：对非数学领域的形式化证明支持尚不完善，需进一步扩展数据集。

如何使用

模型下载：
- 32B 模型：HuggingFace 链接
- 8B 模型：HuggingFace 链接
数据集获取：
- MathOlympiadBench：HuggingFace 链接
快速体验：
- 使用 Python 加载模型并生成证明.

框架技术原理

基座模型：基于 Qwen3-8B/32B 的语言理解能力，构建数学推理基础框架。
专家迭代与强化学习：
- 形式化问题生成：将自然语言数学问题转化为 Lean 4 代码。
- 证明验证与训练：利用新生成的正确证明迭代优化模型，结合强化学习提升性能。
分层式数据合成：自动生成难度递增的证明任务，弥合简单问题与复杂问题之间的差距，提供密集训练信号。
验证器引导的自我修正：通过 Lean 编译器反馈迭代修正证明，模拟人类完善过程，并融入监督微调与强化学习。
模型平均：融合多个训练节点的模型权重，避免后期训练多样性下降，提升鲁棒性。